RANSAC 停止准则的修正：从近似到精确

文章概述

几年以前在自己写RANSAC算法时候， 就发现利用Multi-View Geometry那本圣经中的停止准则来计算迭代次数，似乎不能得到最好的解。 后来面试过一些候选人，他们也发现了这个问题。 但是我从未怀疑过是理论出了问题，况且在读那本Multi-View Geometry一书的时候，我也确信自己是读懂了的。 今年发现这篇文章，真的是有那种感觉，就是发现有问题的地方，应该好好思考，敢于怀疑。好了，说了这么多其实这篇文章很短， 就是修正了RANSAC 算法停止准则中概率的近似计算问题。 文章地址： https://arxiv.org/abs/2503.07829

文章题目：Fixing the RANSAC Stopping Criterion， 由 Johannes Schönberger、Viktor Larsson 和 Marc Pollefeys 发表于今年-- 2025 年。 一作是Colmap的作者。

正题

RANSAC（Random Sample Consensus）自 1981 年由 Fischler 和 Bolles 提出以来，一直是计算机视觉中最常用的鲁棒估计算法之一 。设 s 表示期望我们RANSAC算法的采样中至少能有一次采样点都是内点，也就是能够正确工作的期望概率， 例如0.99。设 P 表示一次采样全部都是内点的概率。我们尝试采样次数N应该满足：
$$\begin{equation} (1 − P )^N \leq 1 − s \end{equation}$$

两边取对数，并且注意到(1 − P ) < 1 ，我们有

$$\begin{equation} N \geq \dfrac{log(1 − s)}{log(1 − P )} \end{equation}$$

原始的paper给定所有内点的概率的计算公式为：

$$\begin{equation} P_a = p^k \end{equation}$$

但是，这其实是一个近似解(Pa中的a表示是一个approximate）。 论文指出，正确的精确（exact）概率应该是：
$$\begin{equation} P_e =\frac{\binom{pn}{k}}{\binom{n}{k}} \end{equation}$$
其实可以等价表示为：
$$\begin{equation} P_e = \prod_{i=0}^{k-1} \frac{n_p - i}{n - i} \end{equation}$$
n 为整体样本数量， pn 是内点数量。如果pn > k,那么P = $P_e$ ,否则P = 0。

效果

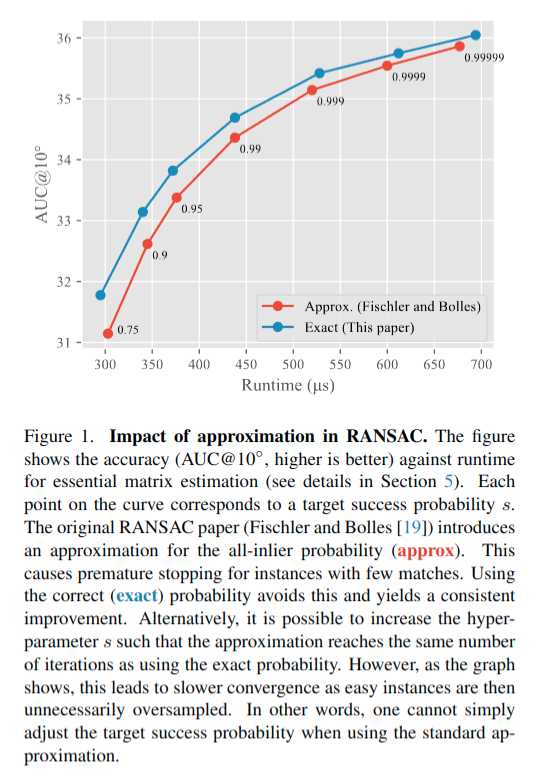
作者实验了使用精确计算和近似计算的效果。

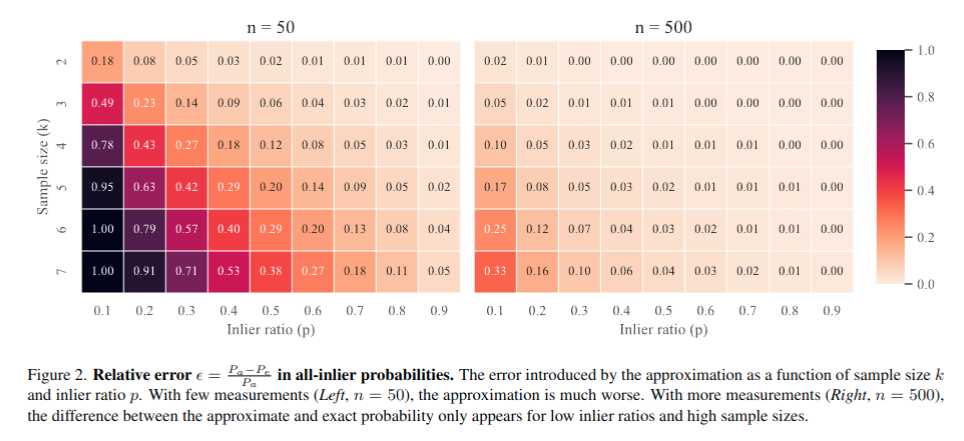
并且分析了pa与pe之间的相对误差关系与内点率和sample 维度K之间的关系，见下图。

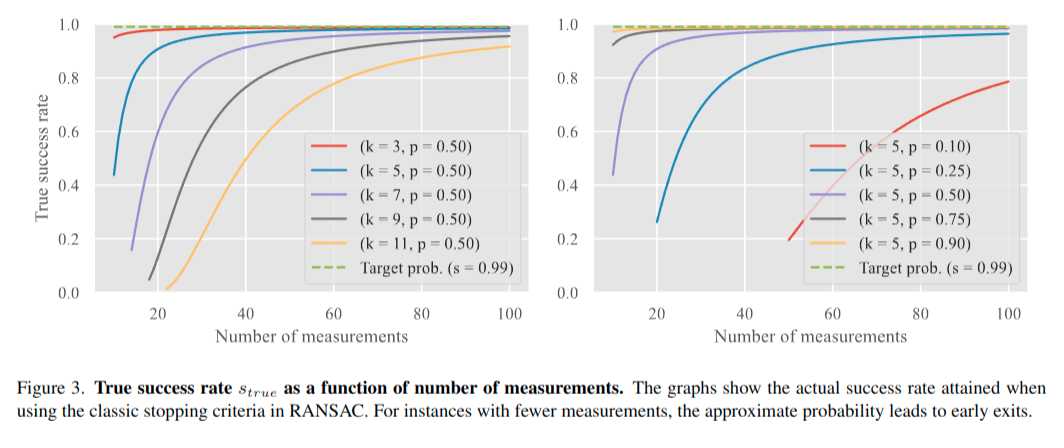
作者还分析了概率估计对真正的s（RANSAC正确工作的概率）的影响

其中
$$\begin{equation} s_{true} = 1 - {(1 - P_e)}^{\frac{log(1 - s)}{log(1−P_a)}} \end{equation}$$

实际影响

最后总结起来，就是使用错误的概率计算方法，导致RANSAC算法在某些场景下表现不佳。

• 欠采样：RANSAC 在挑战性场景中过早停止
• 模型失败：无法找到好的模型
• 性能下降：在低内点比例场景中表现不佳
• 参数K数量：K越大越容易出现错误

下图是我自己写的一个脚本来直观的看下近似估计和精确估计之间，对于迭代次数N的估计差异。

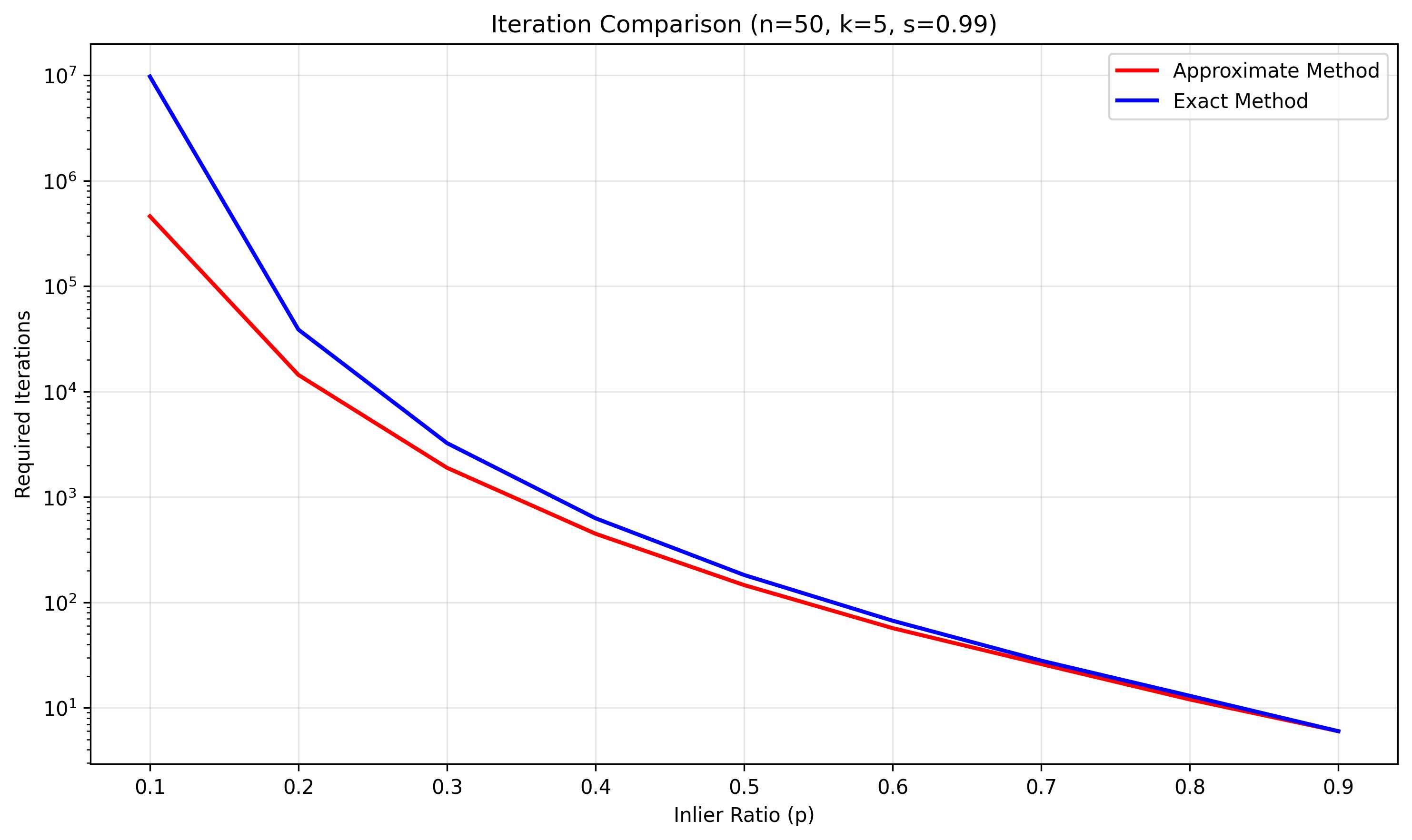
精确停止准则的实现

实现精确概率计算非常简单：

def exact_all_inlier_probability(n, p, k):
    ""计算精确的全内点采样概率""
    pn = int(p * n)  # 内点总数
    if pn < k:
        return 0.0

    probability = 1.0
    for i in range(k):
        probability *= (pn - i) / (n - i)
    return probability

停止准则计算

def compute_iterations(s, P):
    ""计算所需的迭代次数""
    if P >= 1.0:
        return 1
    return math.ceil(math.log(1 - s) / math.log(1 - P))

开源项目影响

论文调查了多个流行的开源项目，发现几乎所有项目都使用了错误的近似方法，包括：

• OpenCV
• scikit-image
• scikit-learn
• COLMAP
• OpenMVG
• ORB-SLAM3

修复的简单性

修正这个问题通常只需要几行代码的改动，但能带来显著的性能提升。

结论与意义

主要贡献

1. 理论分析：首次系统分析了 RANSAC 停止准则中的近似误差
2. 精确解决方案：提出了简单有效的精确概率计算方法
3. 实验验证：在多个计算机视觉问题上验证了改进效果

实际意义

• 在挑战性场景中显著提高模型估计成功率
• 减少灾难性估计失败
• 为计算机视觉社区提供重要的算法修正

局限性

• 精确方法会增加运行时间，特别是在困难场景中
• 未考虑测量噪声、最小求解器稳定性等其他因素
• 未在所有 RANSAC 变体上进行全面测试

未来展望

这项工作为 RANSAC 算法的进一步改进奠定了基础，未来可以：

1. 将精确停止准则集成到所有流行的 RANSAC 实现中
2. 研究其他影响成功概率的因素
3. 开发统一的框架来综合考虑各种影响因素

参考文献：Schönberger, J., Larsson, V., & Pollefeys, M. (2025). Fixing the RANSAC Stopping Criterion. arXiv preprint arXiv:2503.07829.