前言

在 Poisson Surface Reconstruction 表面重建文章中， 提到了使用自身 n 次卷积的 box filter 来作为平滑滤波器来说对指示函数进行平滑，生成梯度场。 那么 box filter 自身的 n 次卷积是什么呢？ 文章里面说用一个方差是采样分辨率的高斯函数是合适的，为什么可以用 box filter 自身 n 次卷积来代替高斯函数是合适的呢？ 下面就这个问题详细进行展开讨论。 因为采用的滤波器会直接影响到算法的数值离散化方式和效率。我们需要在理论和实践上都去理解它。

🧩 一、背景：Poisson 重建中的卷积思想

在 Poisson 重建中，我们要求解一个方程：

$$\Delta \chi = \nabla \cdot \mathbf{V}$$

其中

• $\chi$ 是隐式函数（其 0 等值面为重建表面）
• $\mathbf{V}$ 是由点云法向估计出来的“梯度场”近似。

离散时，我们通常在 三维格点上 近似求解这个方程。此时，$\chi$ 会用 基函数展开：

$$\chi(\mathbf{x}) = \sum_i c_i B(\mathbf{x} - \mathbf{x}_i)$$

这里的 $B(\cdot)$ 就是一个 B-spline(Basis Spline) 核函数。 实际上 box filter 自身 n 次卷积又称为B-spline 核函数,或者称为 B 样条函数。 没错，这个也就是计算机图形学里面那个 B 样条函数，关于B样条函数的术语，可以参考附录B。

B-spline 特点：

• 局部支持（local support）：矩阵稀疏；
• 平滑（smooth）：适合解拉普拉斯方程；
• 可分离（separable）：3D 计算可分为 1D 卷积。

🧱 二、B-spline 和 box filter 的关系

✅ 结论一句话：

B-spline 核函数是 box filter 的多次自卷积结果。

具体地：

$$B_n(x) = \underbrace{(b * b * \cdots * b)}_{n+1 \text{ 次}}$$

其中 $b(x)$ 是 box filter（单位宽度的矩形函数）。

🧮 举例说明

1. 0 阶 B-spline

   $$B_0(x) = \begin{cases} 1 & |x| < \tfrac{1}{2}\\ 0 & \text{otherwise} \end{cases}$$

   这就是一个 box filter。

2. 1 阶 B-spline

   $$B_1(x) = B_0 * B_0$$

   也就是两个 box filter 卷积后的结果，形成一个 三角形核（tent function）。

3. 2 阶 B-spline

   $$B_2(x) = B_1 * B_0$$

   这会变成一个二次平滑的核（光滑的凸形），再往上阶就更平滑。

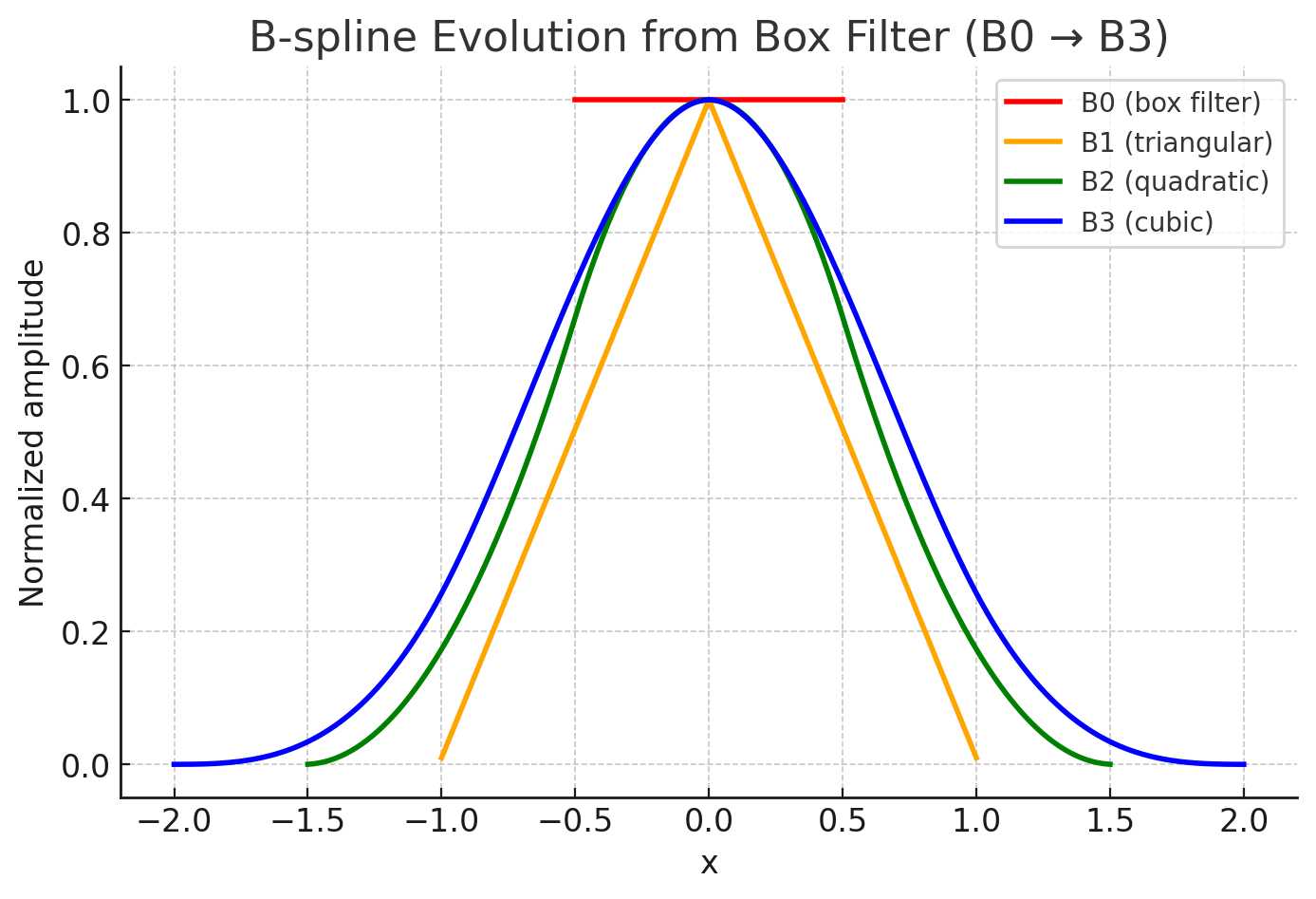
下图是通过Box filter卷积展示的B0-B3的 B-spline 核函数的形状，可以看到3阶 B-spline 的形状已经很像一个gaussian 核函数了。

如果感兴趣box filter 卷积的形状推导和代码示例，可以参考 附录 A，推导 B-spline 的分段表达式

🧠 三、为什么 Poisson 重建里用 B-spline

1. 紧支撑（compact support）：
   每个基函数只影响局部区域（通常一个格点的八邻域）。
2. 可用 box filter 实现快速卷积：
   因为 B-spline = 多次 box filter 卷积，所以在实现上可以利用积分图（summed-area table）或 box filtering 技巧来快速计算梯度、散度和能量项。
   卷积的次数越多，函数越光滑：
3. Poisson 重建里通常用 三次 B-spline（cubic B-spline）， 因为它在 $C^2$ 连续的情况下计算梯度和 Laplace 都很稳定。
   实现上则用 box filter 的多次积分来高效模拟卷积。

• $B_0$：不连续（box）
• $B_1$：连续但不可导
• $B_2$：一次可导
• $B_3$：二次可导（通常使用）

⚙️ 四、数值计算上的意义

当你要计算：

$$\int B(\mathbf{x} - \mathbf{x}_i) B(\mathbf{x} - \mathbf{x}_j)\, d\mathbf{x}$$

这样的项时，
用 box filter 实现比直接算 spline 快得多。
所以在实现中，Poisson 重建经常会：

• 先通过 box filter 累积法向场（V）；
• 再通过 多次 box filter 平滑 得到对应的 B-spline 加权场；
• 最后解线性系统得到系数 $c_i$。

🔍 五、总结对比表

📖 参考文献

• Kazhdan, M., Bolitho, M., & Hoppe, H. (2006).
  Poisson Surface Reconstruction.
• Kazhdan & Hoppe (2013).
  Screened Poisson Surface Reconstruction.

附录 A，推导 B-spline 的分段表达式

一 1 阶 B-spline 是一个三角形核函数

下面给出证明，我们先证明 1 阶 B-spline 是一个三角形核函数。

证明：若

$$b(x)=\begin{cases}1,&|x|<\tfrac12,\\0,&\text{otherwise},\end{cases}$$

则一阶 B-spline （即 $B_1$）定义为 $B_1=b*b$，其解析表达为

$$B_1(x)=\begin{cases} 1-|x|, & |x|<1,\\[4pt] 0, & |x|\ge1. \end{cases}$$

（注意这里 $b$ 的面积为 1，因而 $B_1$ 的峰值为 1，整体积分仍为 1。）

1. 卷积定义

两个函数的卷积：

$$(B_1)(x)=(b*b)(x)=\int_{-\infty}^{\infty} b(t)\,b(x-t)\,dt.$$

由于 $b$ 是指示函数（indicator），可以写成

$$b(t)=\mathbf{1}_{[-\tfrac12,\tfrac12]}(t),\qquad b(x-t)=\mathbf{1}_{[-\tfrac12,\tfrac12]}(x-t).$$

于是被积函数为 1 当且仅当 $t\in[-\tfrac12,\tfrac12]$ 且 $x-t\in[-\tfrac12,\tfrac12]$。

第二个条件等价于 $t\in[x-\tfrac12,x+\tfrac12]$。

因此被积函数为 1 当且仅当

$$t\in I(x)\equiv [-\tfrac12,\tfrac12]\cap[x-\tfrac12,x+\tfrac12].$$

卷积值等于交集 $I(x)$ 的长度（Lebesgue measure）：

$$B_1(x)=\operatorname{length}(I(x)).$$

2. 求交集长度（分段分析）

交集区间上下界是

$$\text{下界}= \max\!\big(-\tfrac12,\; x-\tfrac12\big),\qquad \text{上界}= \min\!\big(\tfrac12,\; x+\tfrac12\big).$$

所以长度为

$$B_1(x)=\min\!\big(\tfrac12,\; x+\tfrac12\big)-\max\!\big(-\tfrac12,\; x-\tfrac12\big),$$

当上界 ≤ 下界 时长度为 0（表示无重叠）。

下面按 $x$ 的范围分情况计算。

情况 A： $x\le -1$

此时区间 $[x-\tfrac12,x+\tfrac12]$ 在 $[-1.5,-0.5]$ 之类，完全落在 $[-∞,-\tfrac12]$ 左侧，与 $[-1/2,1/2]$ 无交集 → $B_1(x)=0$.

情况 B： $-1 < x < 0$

• 上界：$\min(\tfrac12, x+\tfrac12)=x+\tfrac12$（因为 $x+\tfrac12<\tfrac12$）
• 下界：$\max(-\tfrac12, x-\tfrac12)=-\tfrac12$（因为 $x-\tfrac12<-\tfrac12$）

因此

$$B_1(x)=(x+\tfrac12)-(-\tfrac12)=x+1.$$

注意 $x+1=1-|x|$ 在此区间（因为 $|x|=-x$）。

情况 C： $0 \le x < 1$

• 上界：$\min(\tfrac12,x+\tfrac12)=\tfrac12$（因为 $x+\tfrac12\ge\tfrac12$）
• 下界：$\max(-\tfrac12,x-\tfrac12)=x-\tfrac12$

因此

$$B_1(x)=\tfrac12-(x-\tfrac12)=1-x,$$

也就是 $1-|x|$ （在此区间 $|x|=x$）。

情况 D： $x\ge 1$

无重叠，$B_1(x)=0$.

3. 合并分段结果

把上面的各段合并：

$$B_1(x)=\begin{cases} 0, & |x|\ge1,\\[4pt] 1-|x|, & |x|<1. \end{cases}$$

这就是著名的 三角形核（tent function）。

4. 性质检验（可选）

1. 支持：$\mathrm{supp}(B_1)=[-1,1]$（宽度为 2）。
2. 最大值：$B_1(0)=1$。
3. 积分（面积）：

$$\int_{-\infty}^{\infty} B_1(x)\,dx = \int_{-1}^{1} (1-|x|)\,dx = 2\int_{0}^{1} (1-x)\,dx =2\left[x-\tfrac{x^2}{2}\right]_0^1=2\cdot\tfrac12=1,$$

与单个 box 的面积一致（卷积保持总能量/面积）。

4. 导数（分段）：

$$B_1'(x)=\begin{cases} 1, & -1<x<0,\\ -1, & 0<x<1,\\ 0, & \text{elsewhere (in distribution sense at }\pm1,0\text{有不连续点)}. \end{cases}$$

说明 $B_1$ 连续但在 $x=0$ 可导性改变（一次可导不连续）。

5. 直观解释（补充）

• 把宽为 1 的两个单位矩形沿 x 轴滑动相乘并积分；卷积在每个位置 $x$ 上的值就是两个矩形重叠长度。
• 当 $x=0$ 重叠最大（长度=1）；当 $x$ 逐渐移动到 ±1 时重叠线性变为 0，产生线性的上升/下降段 -> 三角形。

二 2 阶和 3 阶 B-spline 核函数的形状

1. 设定与回顾

定义 0 阶（box）函数

$$b(x)=\mathbf{1}_{[-\tfrac12,\tfrac12]}(x)= \begin{cases}1,&|x|<\tfrac12,\\0,&\text{otherwise.}\end{cases}$$

已知

$$B_1(x)=(b*b)(x)=\begin{cases}1-|x|,&|x|<1,\\0,&|x|\ge1,\end{cases}$$

即“三角形核”。

接下来

$$B_2(x)=B_1*b=(b*b)*b, \qquad B_3(x)=B_2*b.$$

卷积定义（1D）：

$$(f*g)(x)=\int_{-\infty}^{\infty} f(t)\,g(x-t)\,dt.$$

2. 详细推导：二阶 $B_2(x)=B_1*b$

写成积分：

$$B_2(x)=\int_{-\infty}^\infty B_1(t)\, b(x-t)\,dt.$$

由于 $B_1(t)$ 在 $|t|<1$ 有值，$b(x-t)$ 在 $|x-t|<\tfrac12$ 有值，因此被积项非零当且仅当

$$t\in[-1,1]\cap[x-\tfrac12,\,x+\tfrac12].$$

所以积分的上下限是

$$\text{下界}=L(x)=\max(-1,\,x-\tfrac12),\qquad \text{上界}=U(x)=\min(1,\,x+\tfrac12),$$

且在这些 $t$ 上被积函数为 $B_1(t)=1-|t|$.

因此

$$B_2(x)=\int_{L(x)}^{U(x)} (1-|t|)\,dt.$$

观察交集何时为空：当 $[x-\tfrac12,x+\tfrac12]$ 与 $[-1,1]$ 无交集时（即 $|x|\ge 1.5$），积分为 0。所以 $B_2$ 的支撑是 $[-3/2,\,3/2]$。

关键断点来自使上下界转变的点：$x=-\tfrac32,\; -\tfrac12,\; \tfrac12,\; \tfrac32$。因此分四段讨论（对称性可只做 $x\ge0$ 再镜像，但这里写出三段中心表达）：

情形 A： $-\tfrac32 \le x < -\tfrac12$

在此区间，$x+\tfrac12<0$ 且 $x-\tfrac12<-1$，因此

$$L(x)=-1,\quad U(x)=x+\tfrac12,\quad\text{并且区间内 }t\le0,$$

所以 $|t|=-t$，被积项 $1-|t|=1+t$。

计算：

$$B_2(x)=\int_{-1}^{\,x+\tfrac12}(1+t)\,dt =\Big[t+\tfrac{t^2}{2}\Big]_{-1}^{x+\tfrac12}.$$

令 $u=x+\tfrac12$，则

$$B_2(x)=\Big(u+\tfrac{u^2}{2}\Big)-\Big(-1+\tfrac{1}{2}\Big) = u+\tfrac{u^2}{2}+\tfrac12.$$

化简（把 $u=x+\tfrac12$ 代回）：

$$B_2(x)=\frac{(x+\tfrac32)^2}{2}, \qquad -\tfrac32\le x<-\tfrac12.$$

情形 B： $-\tfrac12 \le x \le \tfrac12$

此时交集为 $[x-\tfrac12,\,x+\tfrac12]$，并且区间跨过 $t=0$。于是分两段积分（从 $x-\tfrac12$ 到 0，再到 $x+\tfrac12$）：

$$B_2(x)=\int_{x-\tfrac12}^{0} (1+t)\,dt + \int_{0}^{x+\tfrac12} (1-t)\,dt.$$

计算：

$$\int_{x-\tfrac12}^{0}(1+t)\,dt = -\big(x-\tfrac12\big) - \tfrac{(x-\tfrac12)^2}{2},$$ $$\int_{0}^{x+\tfrac12}(1-t)\,dt = \big(x+\tfrac12\big) - \tfrac{(x+\tfrac12)^2}{2}.$$

相加并化简（省略代数中间行）结果为

$$B_2(x)=\tfrac34 - x^2,\qquad |x|\le \tfrac12.$$

（可以验算：在 $x=0$ 时 $B_2(0)=3/4$，在 $x=\pm 1/2$ 时为 $3/4 - 1/4 = 1/2$，与相邻段连续。）

情形 C： $\tfrac12 < x \le \tfrac32$

对称于 A 段，可写出：

$$B_2(x)=\frac{(\tfrac32-x)^2}{2},\qquad \tfrac12<x\le\tfrac32.$$

合并写成分段函数（即最终结果）

$$\boxed{\,B_2(x)=\begin{cases} \frac{(x+\tfrac32)^2}{2}, & -\tfrac32\le x< -\tfrac12,\\[6pt] \tfrac34 - x^2, & |x|\le \tfrac12,\\[6pt] \frac{(\tfrac32-x)^2}{2}, & \tfrac12< x\le \tfrac32,\\[4pt] 0,& |x|>\tfrac32. \end{cases}\,}$$

• 支撑：$[-3/2,\,3/2]$（宽度 3）。
• 在边界处各段值与导数可检查为连续（$C^1$ 连续，即一次连续导数），但二阶导在节点处有间断（这与次数 2 的光滑度一致）。
• 积分 $\int B_2(x)\,dx=1$。

3. 三阶 $B_3$（结果与说明）

三阶可以继续用卷积 $B_3 = B_2 * b$。它的支撑是 $[-2,2]$。分段点出现在 $|x|=0,1,2$。最终的、常见且标准化的闭式分段多项式为：

$$\boxed{\,B_3(x)=\begin{cases} \displaystyle\frac{1}{6}\,(2-|x|)^3, & 1<|x|<2,\\[8pt] \displaystyle\frac{1}{6}\big(4-6x^2+3|x|^3\big), & |x|\le 1,\\[6pt] 0, & |x|\ge 2. \end{cases}\,}$$

（注意公式中出现 $|x|^3$ 保证了关于原点的偶对称性。）

这可以等价写成两段（利用偶性）：

• 当 $0\le |x|\le 1$：
  $$B_3(x)=\frac{4-6x^2+3|x|^3}{6}.$$
• 当 $1<|x|<2$：
  $$B_3(x)=\frac{(2-|x|)^3}{6}.$$

性质检验 / 由卷积得到的理由（概述推导路线）：

• $B_3(x)=\int_{L(x)}^{U(x)} B_2(t)\,dt$（其中 $L,U$ 与上面类似，分段点为 $-2,-1,0,1,2$）。
• 分段时要把积分区间按 $B_2$ 的三段形式拆开（每一段为二次多项式），对每一段做多项式原函数计算并合并，最后化简得到上面的三次多项式表达。
• 连续性：$B_3$ 在节点处连续且一阶、二阶导数也连续（即 $C^2$），这与 degree=3 的 B-spline 的光滑度相符。
• 面积：$\int_{-\infty}^{\infty} B_3(x)\,dx = 1$。

4. 小结（直观与对应表）

• $B_0$（box）：支撑 $[-1/2,1/2]$，不连续。
• $B_1$（三角）：支撑 $[-1,1]$，连续但一阶不可导（$C^0$）。
• $B_2$（二次）：支撑 $[-3/2,3/2]$，$C^1$（一次可导连续）。
• $B_3$（三次）：支撑 $[-2,2]$，$C^2$（二阶导连续），常用于图形/Poisson 重建中因为求二阶导（Laplace）数值稳定。

每升一阶，等价于对 box filter 做一次卷积——函数更宽、平滑度提高，且每段都是对应次数的多项式。

形状绘制

下面通过绘制代码来具体观察一下形状。

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import convolve

def box_filter_1d(resolution=0.01):
    x = np.arange(-0.5, 0.5 + resolution, resolution)
    y = np.ones_like(x)
    return x, y / np.sum(y)

def bspline_1d(order, resolution=0.01):
    x, b = box_filter_1d(resolution=resolution)
    y = b.copy()
    for _ in range(order):
        y = convolve(y, b, mode='full') * resolution
    x_full = np.linspace(-(order + 1) / 2, (order + 1) / 2, len(y))
    return x_full, y / np.max(y)

# 绘制从 box filter 到 cubic B-spline 的演化
plt.figure(figsize=(8, 5))
colors = ['red', 'orange', 'green', 'blue']
labels = ['B0 (box filter)', 'B1 (triangular)', 'B2 (quadratic)', 'B3 (cubic)']

for n, color, label in zip(range(4), colors, labels):
    x, y = bspline_1d(n)
    plt.plot(x, y, color=color, label=label, linewidth=2)

plt.title("B-spline Evolution from Box Filter (B0 → B3)")
plt.xlabel("x")
plt.ylabel("Normalized amplitude")
plt.legend()
plt.grid(True)
plt.show()

• order=0 ：box filter（矩形函数）
• order=1 ：三角形核
• order=2 ：二次平滑核
• order=3 ：三次 B-spline（通常用于 Poisson 重建）

这张图展示了从 box filter（B₀） 到 三次 B-spline（B₃） 的平滑演化过程：

• 红色：B₀，方形脉冲（不连续）
• 橙色：B₁，三角形（一次连续）
• 绿色：B₂，二次平滑（一次可导）
• 蓝色：B₃，三次平滑（两次可导）

你可以看到——每卷积一次，曲线就更光滑、支撑范围更宽。
这就是 B-spline 的核心思想：通过 box filter 的多次卷积实现平滑基函数。

📘 附录 B-spline 的中文术语常见翻译