关于Poisson重建$\partial$符号的理解

初次看到Poisson重建这篇文章的时候，看到他用$\partial M$ 表示表面，当时很困惑，为什么偏导数表示表面？ 这里我觉得有一个概念理解错误的问题。 作者使用$\partial M$ 表示“集合 M 的边界”，而不是“偏导数”。 具体说来， $\partial$其实是数学记号上的“边界符号”（boundary operator），不是偏导数。

一、误解的来源

在 Poisson Surface Reconstruction 论文中（Kazhdan et al., 2006），确实有这样的记号：

$$\partial M \equiv \text{surface of the solid model } M$$

很多人第一次看会以为 “∂” 是偏导符号，但其实这里：

$\partial M$ 表示的是集合 M 的边界（boundary），而不是偏导（partial derivative）。

二、数学背景：拓扑学/几何分析中的边界算子

在**几何拓扑（geometric topology）或流形理论（manifold theory）**中，
“∂” 是标准的边界算子（boundary operator），读作 “boundary of”。

例如：

• 对于二维区域 $M \subset \mathbb{R}^2$，
  它的边界 $\partial M$ 是一条一维曲线；

• 对于三维体积 $M \subset \mathbb{R}^3$，
  它的边界 $\partial M$ 是一个二维表面。

这种“降一维”的对应关系是拓扑学中非常核心的概念。

三、Poisson 重建中为什么要这样写

Poisson Surface Reconstruction 的核心思想是：

我们假设存在一个隐式函数 $\chi(\mathbf{x})$，表示物体的指示函数：

$$\chi(\mathbf{x}) = \begin{cases} 1, & \mathbf{x} \in M \\ 0, & \mathbf{x} \notin M \end{cases}$$

那么，表面就定义为这个体的边界：

$$\partial M = \{ \mathbf{x} \mid \chi(\mathbf{x}) = \text{const} \}$$

或者等价地说：

$$\partial M = \text{zero level set of } \chi$$

四、符号上的逻辑关系

所以 “∂” 在这里不是“偏导”，而是“边界算子”，在几何上表示取边界这个操作。

五、总结一句话

在 Poisson 表面重建中，$\partial M$ 表示“体积 M 的边界表面”，
这个符号来自微分几何与拓扑中的边界算子，
不是偏导数符号，也不是梯度符号。

六、如何理解等值集levelset呢？

第三节我们说，$$\partial M = \text{zero level set of } \chi$$
这个公式如何理解呢？ levelset又是什么？

“等值集 (level set)” 是理解隐式表面、Poisson 重建、甚至很多偏微分方程（PDE）问题的核心概念。
我们一步步把它讲清楚。

6.1 定义：什么是等值集（Level Set）

给一个标量场：

$$f: \mathbb{R}^n \to \mathbb{R}$$

它在空间中每个点都有一个实数值。

那么对某个常数 $c$，**等值集（level set）**定义为：

$$L_c = \{ \mathbf{x} \in \mathbb{R}^n \mid f(\mathbf{x}) = c \}$$

这就是——

所有使函数值等于同一个常数的点的集合。

6.2、低维直观例子

6.3、几何意义：隐式定义的曲面/曲线

你可能见过显式定义的曲面，比如：

$$z = g(x, y)$$

但等值集是一种**隐式定义（implicit form）**的方式：

$$f(x, y, z) = c$$

这两者的关键区别是：

• 显式形式：你把一个变量当作其他变量的函数；

• 隐式形式：你只说哪些点“满足某个条件”属于表面。

这种隐式表示能轻易描述复杂拓扑的表面（例如空洞、分叉），
这就是为什么 Poisson 重建、SDF（有符号距离场）、Level Set 方法 都用隐式表示。

6.4、梯度与法向的关系

在等值集上：

$$f(\mathbf{x}) = c$$

对任意在表面上微小移动 $d\mathbf{x}$，我们有：

$$df = \nabla f \cdot d\mathbf{x} = 0$$

这表示沿着表面移动时，函数值不变，所以：

梯度 $\nabla f$ 总是垂直于等值面。

换句话说：

• 等值集定义了“面”；

• 梯度定义了“面法向方向”。

这正是 Poisson 重建的核心几何关系：

$$\mathbf{n}(\mathbf{x}) \propto \nabla \chi(\mathbf{x})$$

6.5、Poisson 重建中的等值集

在 Poisson Surface Reconstruction 中：

1. 我们定义一个指示函数 $\chi(\mathbf{x})$，
   它大致为：

   $$\chi(\mathbf{x}) = \begin{cases} 1, & \text{inside the object}\\ 0, & \text{outside} \end{cases}$$

2. 表面定义为它的一个等值集：

   $$\partial M = \{ \mathbf{x} \mid \chi(\mathbf{x}) = c \}$$

   通常取 $c = 0.5$ 或某个平均值。

3. 梯度场 $\nabla \chi$ 与点云的法向方向一致，
   Poisson 方程

   $$\Delta \chi = \nabla \cdot \mathbf{V}$$

   用来从散乱的法向场 $\mathbf{V}$ 恢复出隐式函数 $\chi$。

6.6、从几何角度再看一遍

6.7、图像化比喻

想象一座山：

• 山体的高度就是 $f(x, y)$；

• 每条等高线就是一个level set；

• 梯度方向（最陡上升）垂直于等高线；

• 三维时，同理——等高“线”变成等高“面”。

6.8、总结一句话

**等值集（level set）**是标量场中函数值相等的点的集合，
它是表面的一种隐式表示。
在 Poisson 重建中，物体表面就是指示函数的等值集，
梯度方向定义了表面的法向。

接下来我们画一张图，用 Python显示：

• 标量场 $f(x, y)$；

• 几条等值线；

• 梯度方向箭头？
  这样我们可以一眼看出“level set”和“gradient”的几何关系。

# Creating a visualization of a 2D scalar field, its level sets, and the gradient field (quiver).
# The resulting image will be saved to /mnt/data/levelset_plot.png and displayed inline.
import numpy as np
import matplotlib.pyplot as plt
from pathlib import Path

# Grid
nx, ny = 200, 200
x = np.linspace(-2.0, 2.0, nx)
y = np.linspace(-2.0, 2.0, ny)
X, Y = np.meshgrid(x, y)

# Scalar field: a smooth bump (radial)
F = np.exp(-(X**2 + Y**2))

# Compute gradients (partial derivatives)
dx = x[1] - x[0]
dy = y[1] - y[0]
Fy_x, Fy_y = np.gradient(F, dx, dy, edge_order=2)  # returns derivatives along axis 0 and 1
# Note: np.gradient returns (dF/dy, dF/dx) for a 2D array with axes (y, x).
dFdx = Fy_y
dFdy = Fy_x

# Prepare quiver sampling (sparser for clarity)
step = 12
Xq = X[::step, ::step]
Yq = Y[::step, ::step]
dFdx_q = dFdx[::step, ::step]
dFdy_q = dFdy[::step, ::step]

# Normalize gradient vectors for visualization (only direction matters)
mag = np.sqrt(dFdx_q**2 + dFdy_q**2)
nonzero = mag > 1e-12
dFdx_q[nonzero] /= mag[nonzero]
dFdy_q[nonzero] /= mag[nonzero]

# Plotting
fig, ax = plt.subplots(figsize=(7,7))
# Filled contour for scalar field
cf = ax.contourf(X, Y, F, levels=30, alpha=0.9)
# Contour lines (level sets)
cs = ax.contour(X, Y, F, levels=np.linspace(F.min(), F.max(), 8), linewidths=1)
# Highlight a specific level set, e.g., f = 0.5
lvl = 0.5
cs2 = ax.contour(X, Y, F, levels=[lvl], linewidths=2)
# Quiver for gradient (points outward for this radial bump)
q = ax.quiver(Xq, Yq, dFdx_q, dFdy_q, scale=20, pivot='mid')

ax.set_aspect('equal', 'box')
ax.set_title('Scalar field $f(x,y)=e^{-(x^2+y^2)}$ — level sets and gradient directions')
ax.set_xlabel('x')
ax.set_ylabel('y')

# Save figure
out_path = Path('./levelset_plot.png')
plt.tight_layout()
plt.savefig(out_path, dpi=150)
plt.show()

上面代码运行后，会生成下面的图片：

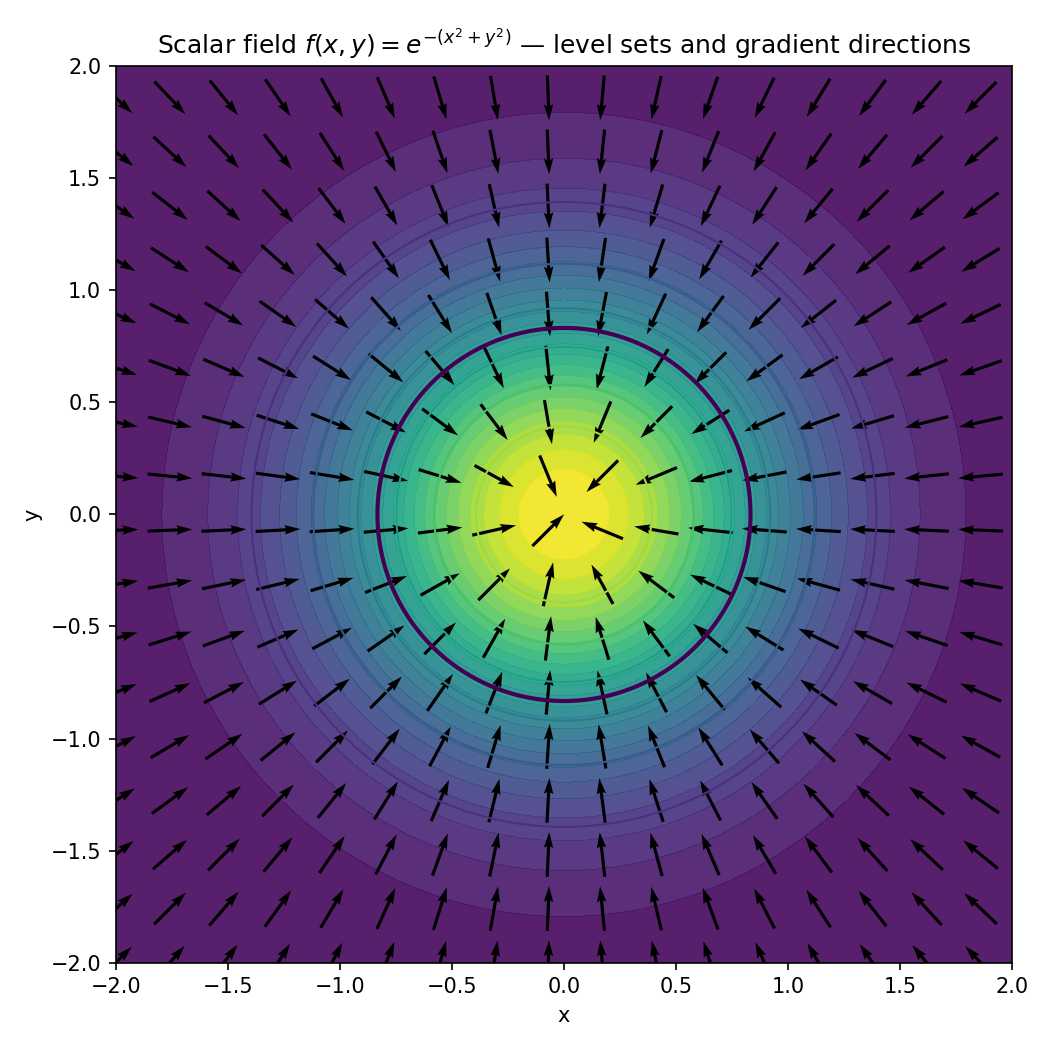
标量场 $f(x,y)=e^{-(x^2+y^2)}$ 的填色图、若干等值线（level sets），以及梯度方向（箭头，quiver）。图中粗线对应 $f=0.5$ 的等值集——这就是一个隐式定义的“曲线/表面”（在 3D 中同理是曲面）；箭头显示梯度方向（指向函数增大的方向），也就是等值集的法向方向。